RC Hochpass berechnen
Rechner und Formeln zur Berechnung der Parameter eines RC Hochpasses
|
|
Zur Berechnung geben Sie die Werte für den Widerstand R, die Frequenz F, die Kapazität C des Kondensators und die Spannug U ein. Dann klicken Sie auf den Button Rechnen .
der Hochpass ist ein Filter, der hohe Frequenzen passieren lässt und niedrige Frequenzen dämpft.
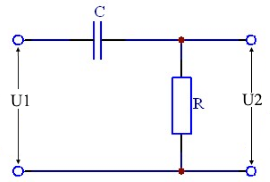
Der Widerstand R und der Kondensator C bilden zusammen den Hochpass. DerKondensator C ist in Serie mit dem Eingang verbunden, der Widerstand R liegt parallel zum Ausgang. Die Spannung U2 am Ausgang wird von der Frequenz abhängen. Bei hohen Frequenzen wird die Spannung U2 fast gleich der Eingangsspannung U1 sein. Bei niedrigen Frequenzen wird die Spannung U2 gegen Null gehen.
Der RC Hochpass hat eine Grenzfrequenz fg, bei der die Spannung U2 um 3dB (0,707) gedämpft wird.
Die Dämpfung Vu wird in Dezibel angegeben und kann für verschiedene Frequenzen berechnet werden.
die Phasenverschiebung φ der Ausgangsspannung U2 gegenĂĽber der Eingangsspannung U1 kann ebenfalls berechnet werden.
der RC Hochpass ist ein einfacher und effektiver Filter, der in vielen Anwendungen eingesetzt wird,
Spannungsverhältnis berechnen
Die Ausgangspannung U2 eines RC Hochpass wird nach der folgenden Formel berechnet.
\[ U_2=U_1 ·\frac{2 · π · f · R · C}{\sqrt{1 + (2 · π · f · R · C)^2}}\]
oder einfacher, wenn XC bekannt ist
\[ U_2=U_1 ·\frac{R}{\sqrt{R^2 + X_C^2}}\]
\[ X_C=\frac{1}{2 π · f ·C}\]
Dämpfung in Dezibel
Die Dämpfung beträgt bei der Resonanzfrequenz 3dB. Sie kann für die verschiedenen Frequenzen nach den Formeln unten berechnet werden. Wenn die Ein- und Ausgangsspannung bekannt sind kann die Dämpfung einfach nach der folgenden Formel berechnet werden.
\[ V_u=20 · lg \left(\frac{U_2}{U_1} \right) \]
Wenn die Spannungen nicht bekannt sind wird die folgende Formel verwendet.
\[V_u=20·lg\left(\frac{2 · π · f · R · C}{\sqrt{1 + (2 · π · f · R · C)^2}}\right)\]
oder einfacher dargestellt
\[ V_u=20·lg\left(\frac{ω · R · C}{\sqrt{1 + (ω · R · C)^2}}\right)\]
Phasenverschiebung
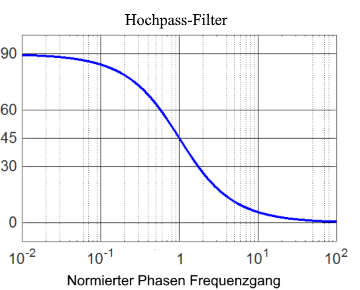
In einem RC Hochpass eilt die Ausgangsspannung der Eingangsspannung, je nach Frequenz um 0° - 90° voraus. Bei der Resonanzfrequenz beträgt die Phasenverschiebung 45°. Bei hohen Frequenzen geht sie gegen 0. Bei niedrigen Frequenzen dreht die Phase in Richtung +90° Die Phasenverschiebung kann mit den folgenden Formel berechnet werden.
\[\displaystyle φ=acos \left(\frac{U_2}{U_1} \right) = \left(\frac{U_a}{U_e} \right)\]
\[\displaystyle φ= arctan \left(\frac{1}{ω · R ·C}\right)\]
Grenzfrequenz
Bei Grenzfrequenz fg bzw. ωg ist der Wert des Amplituden-Frequenzganges (also der Betrag der Übertragungsfunktion) gleich 0,707 Das entspricht –3dB.
\[\displaystyle 0.707= \frac{1}{\sqrt{2}}\] \[\displaystyle ω_g= \frac{1}{R ·C} ⇒\ \ \ \ \ \ f_g=\frac{1}{2·π·R·C}\] \[R=\frac{1}{2·π·f_g·C}\] \[ C=\frac{1}{2·π·f_g·R}\]Impedanz
\[ Z=\sqrt{X_C^2 + R^2} \]Strom
\[ I=\frac{U}{Z} \]Kondensator Spannung
\[ U_C=X_C ·I \]Zeitkonstante
\[ τ=C ·R \]Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz